| |
| |
Digital Signal Processing (DSP) 3
L'analogo della distribuzione delta è nel caso discreto la semplice successione
che vale sempre 0 tranne che nell'origine, dove vale 1. A tale successione daremo
ancora il nome di delta.
Si osservi che se un operatore è lineare e invariante per shift, allora è
caratterizzato dalla successione 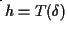 .
.
Infatti ogni T(x) si calcola facendo il prodotto di convoluzione di x con h.
Ad ogni successione x si può associare una Serie di Laurent nella variabile
complessa z, e si ottiene così la z-Trasformata o di Borel:
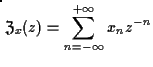
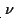 , ottenere
una successione di valori x, di applicarvi un operatore T lineare ed invariante per
shift, ottenendo una successione y, che quindi fornisce un segnale continuo
in uscita.
, ottenere
una successione di valori x, di applicarvi un operatore T lineare ed invariante per
shift, ottenendo una successione y, che quindi fornisce un segnale continuo
in uscita.
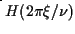 ove
ove 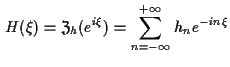 e
e 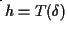
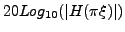 facendo variare il
parametro
facendo variare il
parametro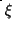 tra 0 e 1, che corrisponde a fare variare la frequenza
tra 0 e metà della frequenza di campionamento, cioè fino alla frequenza di Nyquist.
tra 0 e 1, che corrisponde a fare variare la frequenza
tra 0 e metà della frequenza di campionamento, cioè fino alla frequenza di Nyquist.
Per esempio, se h ha solo un numero finito di termini non nulli (filtri FIR, vedi più avanti) usando maple, bastano questi due comandi:
v:=readdata("/tmp/dati.fir",float);
plot(20*log10(abs(add(evalf(v[k+1]*exp(-Pi*I*x*(k-1))),k=1..v[1]))),x=0..1);
(potete copiare il relativo maple worksheet o vedere l'esempio)
Analogamente in octave o in matlab si può ottenere un simile grafico con questo script
risposta.m e comunque ci sono appositi comandi che vediamo in dettaglio più avanti.
Si noti che questa volta nel file solo_dati.fir non si deve mettere al primo posto il numero di elementi del filtro, che octave
o in matlab calcolano automaticamente man mano che leggono i dati.
|
|