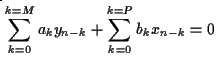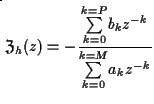 |
Filtri digitali |
|
Digital Signal Processing (DSP) 4
Uno dei problemi importanti nella elaborazione dei suoni, è che spesso
l'elaborazione deve essere fatta in tempo reale.
Questo vuol dire che sono di particolare importanza quelle trasformazioni che
permettono una rapida elaborazione numerica.
Come si è visto, il calcolo di un operatore lineare invariante per shift,
comporta la convoluzione con una successione assegnata. Se questa successione
è formata da un numero finito (e non troppo elevato) di termini, il calcolo
non presenta difficoltà eccessive.
I filtri che si ottengono così sono detti FIR (= Finite Impulse Response,
perchè la risposta alla delta è formata da un numero finito di termini).
Dalle considerazione fatte emerge in particolare che per progettare un filtro FIR
occorre trovarne i coefficienti in modo da ottenere la richiesta risposta in frequenza,
e questo è allora un problema di interpolazione numerica affrontabile con
numerose tecniche note.
Sembrerebbe che nvece i filtri in cui si deve fare la convoluzione con una
successione formata da infiniti termini (in pratica una successione lunghissima)
sfuggano alla possibilità della elaborazione in tempo reale, ma per fortuna
non è sempre così: c'è un' altra possibilità.
Consideriamo l'equazione alle differenze finite:
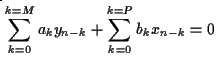Se si assegna la successione x e si considera y come incognita, assegnatiM valori
consecutivi, la y si calcola dall'equazione alle differenze senza difficoltà.
La dipendenza di y da x è lineare, ossia in questo modo si è definito
un operatore T che manda x in y, lineare, invariante per shift, facilmente calcolabile.
La scoperta interessante è che:
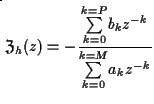Quindi anche operatori T caratterizzati da una successione h, infinita possono essere
calcolati rapidamente quando corrispondono a questi tipi di equazioni di differenze
finite, e si ottengono allora i filtri IIR (Infinite Impulse Response), il cui
disegno (che qui neppure accenneremo) può essere fatto adattando parecchie
tecniche usate nel disegno dei filtri analogici.
|
Laboratorio Sperimentale di Matematica Computazionale - parte II
Sergio Steffè - AA 2015/2016 - PISA |
|
